Обозначение натуральных чисел

В древнее время люди пытались делать запись количества предметов. Это были простые палочки, сколько начертано палочек, столько предметов:

l – одна палочка означала 1 предмет;

ll – 2 предмета; lll – 3 предмета и т.д.

Жители древнего Египта приняли за обозначение сложные и объемные символы, которые могли занимать на дорогом папирусе очень много места и выглядели в виде замысловатых картин.

Привычные для обихода цифры были придуманы еще 1500 лет назад в Индии. Оттуда арабы привезли незнакомые символы в Европу. Простота написания и узнаваемость сделала такие символы распространенными настолько, что современный человек продолжает ими пользоваться. Сейчас эти символы называют арабскими цифрами.

При помощи цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 можно сделать запись какого угодно натурального числа.

Для запоминания!

Само число 0 не принимается за натуральное, потому что не участвует в счете. Эта цифра только служит для записи других натуральных чисел: 10, 20, 30 и т.д.

Множество натуральных чисел

Бесконечное множество натуральных чисел обозначают на письме буквой Ν:

Ν = { 1, 2, 3, 4, 5, 6, 7… }

Упорядоченную последовательность натуральных чисел называют натуральным рядом:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13…

Из записи понятно, что каждое следующее натуральное число ряда больше предыдущего на единицу.

Пример

Сколько чисел находится в натуральном ряду между числами:

а) 2 и 7;

б) 12 и 19.

Решение

а) запишем натуральный ряд 2, 3, 4, 5, 6, 7; между числами 2 и 7 находится 4 числа.

б) запишем натуральный ряд 12, 13, 14, 15, 16, 17, 18, 19; между числами 12 и 19 находится 6 чисел.

Систему счета, которой принято у нас пользоваться называют десятичной позиционной.

Название десятичная исходит от количества цифр. В каждом разряде 10 единиц и они образуют каждый следующий старший разряд. А вот позиционной система считается потому, что крайне важно место записи числа, т.е. разряд, в котором она записана.

Внимание!

Так натуральное число записывать можно и в виде разрядных слагаемых.

Числа 1, 10, 100, 1000, 10 000… называют разрядными единицами.

Числа классифицируют по количеству знаков.

• Однозначными называют те, что имеют в своей записи один знак, это числа от 1 до 9.
• Двузначные числа имеют в своем составе 2 знака: 23, 26, 68, 97.
• Соответственно, трехзначные числа имеют 3 знака (129, 485, 692, 912), а четырехзначные – 4 знака (2598, 3897, 6598).

Все числа, начиная с двузначных и далее называют многозначными.

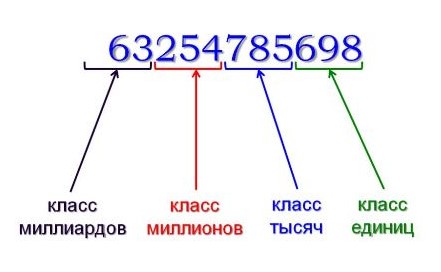
Читать многозначное число нужно правильно, справа налево, при этом разбивая их на группы по 3 цифры. Такие группы именуют классами.

Справа первые 3 цифры означают класс единиц, вторые – класс тысяч, далее класс миллионов и миллиардов. То место, которое цифра занимает при записи числа, называют разрядом.

Поэтому, если считать справа налево, то получаем разряды единиц, десятков, сотен, тысяч.

Например

Число 6078 имеет 8 единиц разряда единиц, 7 единиц разряда десятков, 0 единиц разряда сотен и 6 единиц разряда тысяч.

Как правильно прочитать многозначное число 7 000 125 654: «семь миллиардов сто двадцать пять тысяч шестьсот пятьдесят четыре».

Внимание!

В классе миллионов во всех разрядах этого числа стоят нули, поэтому при чтении опускают название этого класса.

Порядок чтения натуральных чисел

1 шаг

Мысленно число разбивают на классы и читать начинают с конца записи (справа налево).

2 шаг

Названия классов записывают, начиная с самого меньшего (справа-налево) – единицы, тысячи, миллионы и т.д..

3 шаг

 Читается число с самого старшего класса, с указанием названия разрядных единиц и класса.

4 шаг

 Если разряд пуст (стоит 0), то его пропускают.

Например

Надо прочитать многозначное число 360 012 056:

• 360 – триста шестьдесят миллионов (класс миллионов);
• 012 – двенадцать тысяч (класс тысяч);
• 056 – пятьдесят шесть (класс единиц).

Итого: триста шестьдесят миллионов двенадцать тысяч пятьдесят шесть.

Другие примеры чтения чисел:

300 800 – триста тысяч восемьсот;

7 000 009 – семь миллионов девять;

15 000 003 000 – пятнадцать миллиардов три тысячи.

Сокращения в записи чисел

Для простоты записи многозначных чисел приняты распространенные сокращения.

Например

2 000 – 2 тыс. (две тысячи);

56 000 000  – 56 млн. (пятьдесят шесть миллионов);

5 000 000 000  – 5 млрд. (пять миллиардов).

Запись натуральных чисел в виде суммы разрядных слагаемых

Пример

Если разбить число 6 459 328 на классы и разряды, то выглядеть это будет так:

Миллионы	0 0 6	Сотни миллионов Десятки миллионов Миллионы
Тысячи	4 5 9	Сотни тысяч Десятки тысяч тысячи
Тысячи	3 2 8	Сотни Десятки Единицы

Это число также можно представить как сумму:

6 459 328 = 6 000 000 + 400 000 + 50 000 + 9 000 + 300 + 20 + 8.