Отрезок. Длина отрезка. Треугольник

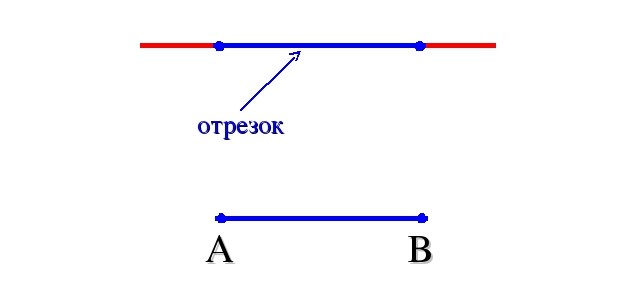
Если на чертеже обозначить две произвольные точки A и B, соединить их прямой линией, то получится отрезок AB. В этом случае точки A и B считают концами отрезка.

Определение

Отрезок — это часть прямой линии, которая ограничена точками на ней.

Через две точки на плоскости можно провести прямую и только одну.

Читать название отрезка можно как слева направо, так и наоборот, главное, правильно обозначить концы отрезка. Правильно будет как отрезок AB, так и отрезок BA.

На примере можно рассмотреть, как точки могут располагаться относительно отрезка АВ. Возьмем произвольные точки Е, N, M.

Точка N лежит на отрезке AB, записывают такой случай так N∈AB. Читать такую запись надо так: «Точка N принадлежит отрезку AB».

В свою очередь точка N делит отрезок AB на два других: AN и NB.

Другие точки E и M не лежат на отрезке AB, поэтому записывают данные так: E∉ AB, M∉ AB. А читается запись: «Точки E и M не принадлежат отрезку AB».

Длина отрезка

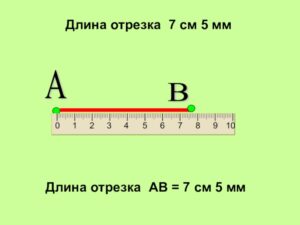
Расстояние между точками A и B называют длиной отрезка.

Например

Длина отрезка АВ равна 7 сантиметром 5 милиметров

Записать это можно следующим образом: АВ = 7,5 см

Вспомни!

Единицы измерения длины — миллиметры (мм), сантиметры (см), дециметры (дм), метры (м), километры (км).

• 1 см— 10 мм
• 1 дм — 10 см
• 1 м — 100 см
• 1 км — 1000 м

Свойство длины отрезка

Если на том же отрезке AB обозначить точку С, то длина отрезка будет ровняться сумме двух отрезков: AB = AС + СB.

Треугольник

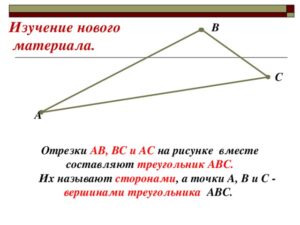
Если нанести на плоскости произвольные три точки А, В, С и соединить их последовательно прямыми, получается геометрическая фигура – треугольник.

Определение

Треугольник — фигура, образованная путем соединения трех точек, не лежащих на одной прямой.

Обозначение ΔАВС читают как «Треугольник АВС».

На треугольнике обозначены его вершины – А, В, С. А отрезки АВ, ВС, АС называют сторонами треугольника.

Виды треугольника

Треугольники для удобства классифицируют по размеру образованных углов:

• прямоугольный –  это тот, у которого один из углов равен 90˚
• тупоугольный – это тот, у которого один из углов превышает значение 90˚
• остроугольный – это тот, у которого все углы менее 90˚

По длине сторон треугольники также разделяют на:

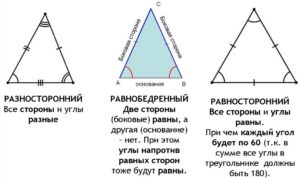
• равносторонний – это тот, у которого все сторону имеют одинаковую длину;
• равнобедренный – это тот, у которого две стороны одинаковой длины;
• разносторонний – это тот, у которого все стороны имеют разную длину.

Периметр треугольника

 У треугольника можно рассчитать периметр.

Определение

Периметр треугольника — сумма длин всех его сторон.

Например

Треугольник ΔАВС имеет стороны АВ, ВС, СА. Тогда формула для вычисления периметра будет выглядеть так:

PΔАВС = АВ + ВС + СА.

Задача

Определите периметр треугольника АВС со сторонами АВ=4 см, ВС=8 см, СА= 9 см.

Решение

РΔАВС = АВ + ВС + СА

РΔАВС= 4+8+9= 21 (см).

Ответ:

РΔАВС = 21 см.