Плоскость. Прямая. Луч

Плоскость

В математике понятие плоскости имеет несколько другое определение. Математическая плоскость не ограничивается размерами, она считается бесконечной.

На плоскости возможно разместить любую произвольную фигуру, даже просто точку.

Прямая

Множество точек, которые последовательно соединены между собой, называют линией.

Линия может иметь различную форму: прямая, кривая, ломаная, разомкнутая.

Определение

Непрерывная (бесконечная) линия, которая не имеет искривлений, называется прямой.

Обозначение прямой

Прямую принято обозначать при помощи строчных букв латинского алфавита: a, h, o, b, l …

Если на прямой обозначить точки А и С, то говорят, что эти точки принадлежат прямой или лежат на ней. При этом саму прямую теперь можно обозначить названием этих точек.

Пример

Прямая АB.

Если же на прямой обозначить большее количество точек, то линию можно назвать любой комбинацией этих точек.

Например

Прямой A принадлежат точки S, N, K, L. Тогда  ее можно назвать A, SL, SK, SN, NK, KL, NL.

Запомни!

 Через две точки на плоскости можно провести единственную прямую.

Свойства прямой

Если на плоскости нанести прямую, то она разделит ее на две полуплоскости.

При этом говорят, что точки А и В принадлежат одной полуплоскости, а вот точки А и С –  разным полуплоскостям.

Расположение прямой на плоскости

Расположение прямых на плоскости относительно друг друга может быть разным.

Определение

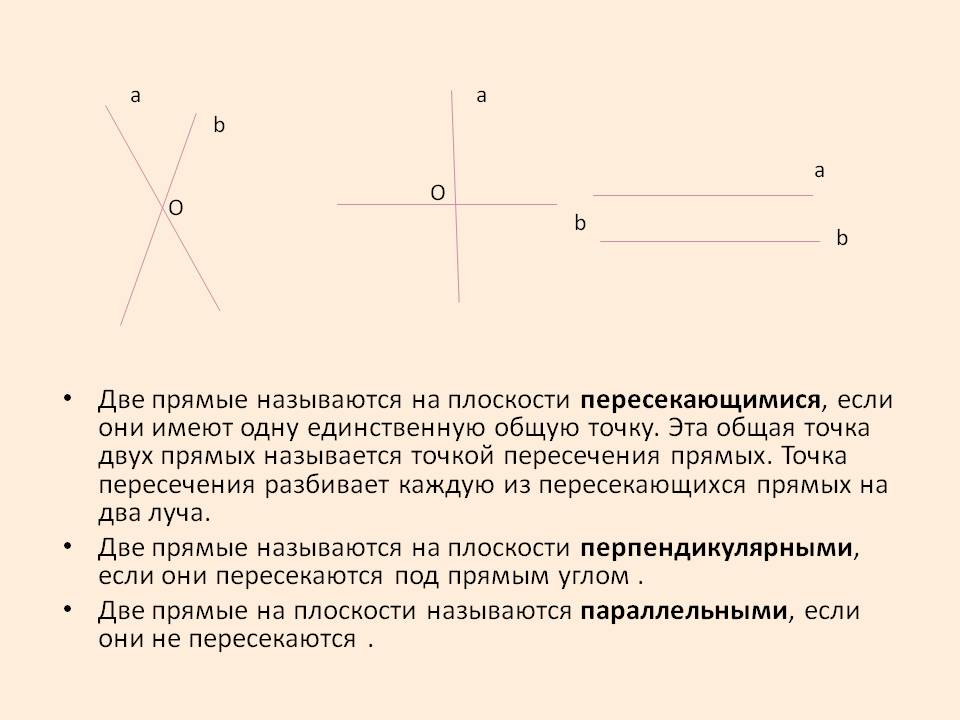
Если две линии пересекаются и имеют общую точку, они называются пересекающимися.

В этом случае у них есть общая точка.

Например

Прямые а и b пересекаются в единой точке o, а эта точка разделяет обе прямые на две части.

Определение

Точка o является точкой пересечения этих прямых а и b. 

Если у заданных прямых нет ни одной общей точки, такие прямые на пересекаются на плоскости.

Определение

Если две линии не имеют общих точек, они являются параллельными.

Если две линии пересекаются в точке и при этом образуют прямой угол, они являются перпендикулярными.

Луч

Если отрезок СD продлить за точку D без ограничения, то получится новая математическая фигура – луч.

Точку С называют началом луча.

Определение

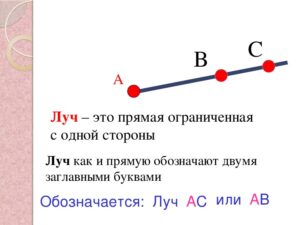
Луч – это прямая, которая (имеет начало) ограничена с одной стороны точкой, но не имеет конца.

Луч имеет следующие свойства:

• имеет свое начало, но не имеет конца;
• имеет направление;
• не имеет размера, поскольку бесконечен.

Если отрезок AB продлить неограниченно за точку C,  получится луч AB, у которого началом служит точка A.

Обозначение луча

При записи луч обозначают большими буквами латинского алфавита. На первое место ставят точку, которая служит началом луча, а на второе – любую другую точку, которая принадлежит этому лучу.

Если на прямой AC обозначить произвольную точку B, то она разделит прямую на два луча. При этом говорят точка B делит прямую AC на два луча — AB и B.

Определение

Лучи, которые образовались при разделении прямой произвольной точкой, принадлежащей этой прямой, называются дополнительными друг другу.

Лучи, берущие начало в одной точке и направленные в одну и ту же сторону, называют совпадающими.

AP и PC — дополнительные друг другу лучи;

AP и AС — совпадающие лучи;

CP и CA — также совпадающие лучи.