1 вариант ОГЭ по математике — демоверсия 2025 года

Подготовка к ОГЭ по математике требует не только знаний школьной программы, но и умения работать с экзаменационным форматом. 1 вариант ОГЭ по математике в демоверсии 2025 года позволяет ученикам ознакомиться с типами заданий, проверить свои силы и отработать навыки решения задач. В статье разберем, как использовать этот инструмент для подготовки, рассмотрим примеры заданий и дадим советы по успешной сдаче экзамена.

Что такое демоверсия 1 варианта ОГЭ по математике?

Пробный вариант экзаменационной работы, составленный на основе актуального содержания ОГЭ, — это демоверсия. Она включает полный перечень заданий, соответствующих требованиям образовательных стандартов.

Основные особенности демоверсии 2025 года:

Разделение на части:

• Часть 1: 19 задач с краткими ответами.
• Часть 2: 6 задач, где требуется развернутый ответ.

Темы заданий: алгебра, геометрия, теоретическая вероятность и текстовые задачи.

Цели демоверсии: помочь ученикам понять структуру экзамена, отработать типовые задания и оценить свой уровень подготовки.

Как скачать и пройти 1 вариант ОГЭ по математике?

Инструкция по работе с демоверсией:

1. Скачайте документ. Демоверсии доступны на официальных ресурсах, таких как ФИПИ или образовательные платформы.
2. Ознакомьтесь со структурой. Внимательно изучите содержание, включая типы заданий и время на выполнение.
3. Решайте задания. Начните с первой части, постепенно переходя ко второй, чтобы тренировать навыки развернутого ответа.
4. Проверяйте результаты. Сравнивайте свои ответы с эталонными решениями.

ЧАСТЬ 1.

Прочитайте внимательно текст и выполните задания.

На плане изображён дачный участок по адресу: п. Сосновка, ул. Зелёная, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота. При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв. м, а чуть подальше — жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведёт дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м × 1 м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.

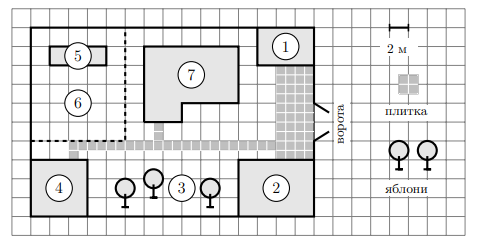
ЗАДАНИЕ 1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр без пробелов, запятых и других символов.

Объекты	гараж	сарай	жилой дом	теплица
Цифры

• Ответ

   

  2175

ЗАДАНИЕ 2. Тротуарная плитка продаётся в упаковках по 7 штук. Сколько упаковок плитки понадобилось, чтобы выложить площадку между сараем и гаражом?

• Ответ

   

  6

ЗАДАНИЕ 3. Найдите периметр фундамента жилого дома. Ответ дайте в метрах

• Ответ

   

  36

ЗАДАНИЕ 4. Сколько процентов от площади всего участка занимают строения (жилой дом, гараж, сарай, баня)? Ответ округлите до целого

• Ответ

   

  29

ЗАДАНИЕ 5. Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв. м, а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.

Номер магазина	Расход краски	Масса краски в одной банке	Стоимость одной банки краски	Стоимость доставки заказа
1	0,6 кг/кв. м	5 кг	2 400 руб.	400 руб.
2	0,4 кг/кв. м	4 кг	2 300 руб.	600 руб.

• Ответ

   

  55800

ЗАДАНИЕ 6. Найдите значение выражения 

• Ответ

   

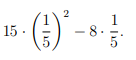
  -1

ЗАДАНИЕ 7. Одно из чисел 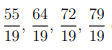отмечено на прямой.

Какое это число?

• Ответ

   

  2

ЗАДАНИЕ 8. Найдите значение выражения

• Ответ

   

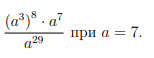
  49

ЗАДАНИЕ 9. Найдите корень уравнения

• Ответ

   

  -14

ЗАДАНИЕ 10. Родительский комитет закупил 20 пазлов для подарков детям в связи с окончанием учебного года, из них 14 с машинами и 6 с видами городов. Подарки распределяются случайным образом между 20 детьми, среди которых есть Вася. Найдите вероятность того, что Васе достанется пазл с машиной.

• Ответ

   

  0,7

ЗАДАНИЕ 11. Установите соответствие между функциями и их графиками.

• Ответ

   

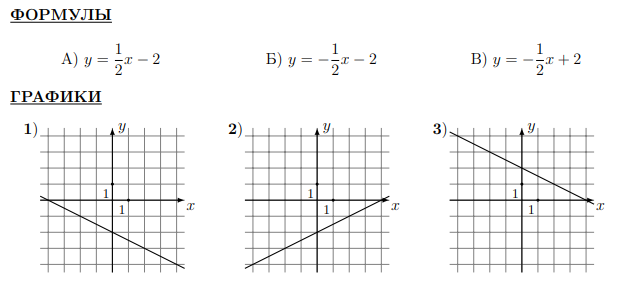
  213

ЗАДАНИЕ 12. В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле 𝐶 = 6000 + 4100𝑛, где 𝑛 — число колец, установленных в колодце. Пользуясь этой формулой, рассчитайте стоимость колодца из 10 колец.

Ответ дайте в рублях.

• Ответ

   

  47000

ЗАДАНИЕ 13. Укажите решение системы неравенств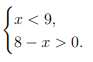

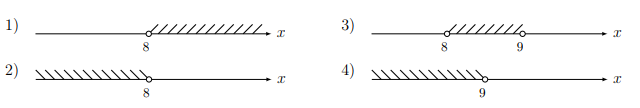
• Ответ

   

  2

ЗАДАНИЕ 14. В амфитеатре 11 рядов. В первом ряду 16 мест, а в каждом следующем на 3 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

• Ответ

   

  341

ЗАДАНИЕ 15. В треугольнике 𝐴𝐵𝐶 известно, что 𝐴𝐵 = 𝐵𝐶, ∠𝐴𝐵𝐶 = 106∘. Найдите угол 𝐵𝐶𝐴.

Ответ дайте в градусах

• Ответ

   

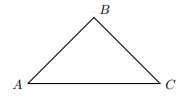
  37

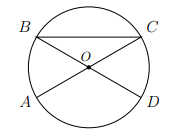
ЗАДАНИЕ 16. В окружности с центром в точке 𝑂 отрезки 𝐴𝐶 и 𝐵𝐷 — диаметры. Угол 𝐴𝑂𝐷 равен 148∘. Найдите угол 𝐴𝐶𝐵.

Ответ дайте в градусах.

• Ответ

   

  16

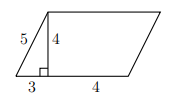
ЗАДАНИЕ 17. Найдите площадь параллелограмма, изображённого на рисунке.

• Ответ

   

  28

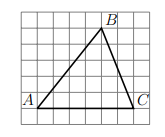
ЗАДАНИЕ 18. На клетчатой бумаге с размером клетки 1×1 изображён треугольник 𝐴𝐵𝐶. Найдите длину его средней линии, параллельной стороне 𝐴𝐶.

• Ответ

   

  3

ЗАДАНИЕ 19. Какое из следующих утверждений верно?

1. Площадь треугольника меньше произведения двух его сторон.
2. Диагонали ромба равны.
3. Тангенс любого острого угла меньше единицы.

В ответ запишите номер выбранного утверждения.

• Ответ

   

  1

ЧАСТЬ 2.

ЗАДАНИЕ 20. Решите уравнение (𝑥 − 2)(𝑥2 + 6𝑥 + 9) = 6(𝑥 + 3).

• Ответ

   

  -4, ±3

ЗАДАНИЕ 21. Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 51 минуту, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 251 км, скорость первого велосипедиста равна 10 км/ч, скорость второго — 20 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

• Ответ

   

  173

ЗАДАНИЕ 22. Постройте график функции

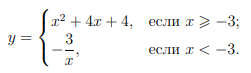
Определите, при каких значениях 𝑚 прямая 𝑦 = 𝑚 имеет с графиком одну или две общие точки.

• Ответ

   

  𝑚 = 0, 𝑚 ⩾ 1

ЗАДАНИЕ 23. Прямая, параллельная стороне 𝐴𝐶 треугольника 𝐴𝐵𝐶, пересекает стороны 𝐴𝐵 и 𝐵𝐶 в точках 𝑀 и 𝑁 соответственно, 𝐴𝐵 = 76, 𝐴𝐶 = 38, 𝑀𝑁 = 28.

Найдите 𝐴𝑀.

• Ответ

   

  20

ЗАДАНИЕ 24. В трапеции 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶 диагонали пересекаются в точке 𝑃.

Докажите, что площади треугольников 𝐴𝑃 𝐵 и 𝐶𝑃 𝐷 равны.

ЗАДАНИЕ 25. Середина 𝑀 стороны 𝐴𝐷 выпуклого четырёхугольника 𝐴𝐵𝐶𝐷 равноудалена от всех его вершин. Найдите 𝐴𝐷, если 𝐵𝐶 = 18, а углы 𝐵 и 𝐶 четырёхугольника равны соответственно 132∘ и 93∘.

• Ответ

   

  18√2

Примеры заданий из демоверсии 1 варианта ОГЭ

Пример 1. Текстовая задача:

На плане изображен дачный участок. Определите, сколько упаковок плитки нужно, чтобы вымостить площадку между сараем и гаражом, если в одной упаковке 7 плиток.

Решение:

• Найдите площадь площадки: 6 м × 4 м = 24 м².
• Посчитайте количество плиток: 24 плитки (по 1 м² каждая).
• Рассчитайте число упаковок: 24÷7= 4 упаковки.

Ответ: 4 упаковки.

Разбор задач и ответы на 1 вариант ОГЭ

• Типичная задача: найдите вероятность, что Вася получит пазл с машиной.
• Всего пазлов: 20.
• Пазлов с машинами: 14.
• Вероятность: P= 1420= 0.7.

Ответ: 70%.

Типичные ошибки при решении задач ОГЭ по математике

При подготовке к ОГЭ по математике многие ученики сталкиваются с трудностями, которые можно было бы легко избежать. Разберем основные ошибки, которые снижают результаты экзамена, и способы их устранения.

Невнимательность к условию задачи

Очень часто ученики спешат перейти к решению задачи, не дочитав условия до конца. Это приводит к путанице в данных и неверному выбору формул или методов решения. Например, в задачах на проценты важно четко понять, к чему относится искомое значение — к начальному числу или к его части.

Ошибки в арифметике

Даже если метод решения выбран правильно, ошибки в простых вычислениях могут свести все усилия на нет. Пример: забытая запятая или неправильно выполненное умножение часто становится причиной неверного ответа.

Отсутствие проверки решения

Некоторые ученики полностью игнорируют проверку своих расчетов, особенно если уверены в правильности ответа. Однако простая перепроверка результатов помогает заметить мелкие, но критичные ошибки.

Чтобы избежать этих проблем, при чтении задачи выделяйте ключевые данные, подчеркивайте числа и условия. После решения обязательно вернитесь к задаче и перепроверьте свой результат, чтобы убедиться в его корректности.

Советы по эффективной подготовке к ОГЭ по математике

Регулярности и системного подхода требует подготовка к ОГЭ. Вот несколько рекомендаций, которые помогут выстроить грамотный план занятий.

Занимайтесь регулярно

Лучше всего выделять для подготовки 3-4 дня в неделю, уделяя занятиям по 1–1,5 часа. Такая частота позволяет не перегружаться, но при этом поддерживать учебный ритм и систематизировать знания.

Используйте онлайн-тренажеры

Платформы, такие как “Решу ОГЭ” и “Онлайн Гимназия № 1”, предлагают задания, соответствующие реальным экзаменационным вопросам. Вы можете тренироваться в удобное время, решая как типовые задачи, так и сложные примеры, требующие повышенного внимания.

Анализируйте свои ошибки

Каждая ошибка — это шанс улучшить знания. После решения теста разберите все задачи, где вы ошиблись: найдите правильное решение, поймите, почему вы допустили промах, и повторите аналогичные задачи.

Уделяйте внимание сложным темам

Часто сложными оказываются текстовые задачи или разделы геометрии. Эти темы требуют не только теоретических знаний, но и практического применения формул и методов. Регулярно возвращайтесь к этим заданиям, чтобы закрепить навыки.

Пример: если текстовые задачи кажутся слишком трудными, начните с простых примеров, постепенно увеличивая сложность. Это поможет развить уверенность и логику.

Как улучшить результаты на ОГЭ по математике?

Если вы хотите получить высокий балл на экзамене, важно не только знать материал, но и правильно организовать процесс подготовки и сам экзамен.

Практикуйтесь на реальных задачах

Регулярно решайте как демоверсии ОГЭ, так и тренировочные варианты из открытого банка заданий ФИПИ. Это позволит привыкнуть к формату экзамена, понять структуру заданий и научиться распределять время.

Работайте с наставником

Индивидуальные занятия с репетитором помогают глубже разобраться в сложных темах и устранить пробелы в знаниях. Репетитор подскажет, как правильно решать задачи и подготовит к экзамену с учетом ваших особенностей.

Правильно распределяйте время на экзамене

Время на ОГЭ ограничено, поэтому важно подходить к его распределению грамотно. Например, на первую часть, которая включает задачи с кратким ответом, стоит выделить около 70% времени. Оставшееся время нужно оставить для сложных задач второй части, где требуется развернутый ответ.

Перед экзаменом потренируйтесь решать задачи с таймером, чтобы привыкнуть к ограничению по времени. Это поможет снизить стресс и улучшить результаты.

1 вариант ОГЭ по математике в демоверсии 2025 года — это эффективный инструмент для подготовки к экзамену. Регулярная практика, использование тренажеров и анализ ошибок помогут добиться высоких результатов.

Главное — подходите к подготовке системно: занимайтесь регулярно, комбинируйте самостоятельные занятия с помощью учителей или репетиторов. Помните, что качественная подготовка — это залог успешной сдачи экзамена и уверенности в своих знаниях.