10 вариант ОГЭ
по математике

ЧАСТЬ 1.

Прочитайте внимательно текст и выполните задания.

Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получаются два равных листа формата А1. Если лист А1 разрезать так же пополам, получаются два листа формата А2, и так далее.

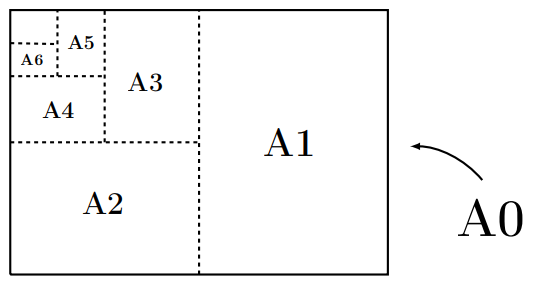
Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта при изменении формата листа.

ЗАДАНИЕ 1. В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А2, А3, А5 и А6.

Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов. А2 А3 А5 А6

В бланк ответов перенесите последовательность четырёх цифр без пробелов, запятых и других дополнительных символов.

• Ответ

   

  2413

ЗАДАНИЕ 2. Сколько листов формата А5 получится из одного листа формата А3?

• Ответ

   

  4

ЗАДАНИЕ 3. Найдите ширину листа бумаги формата А0. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

• Ответ

   

  840

ЗАДАНИЕ 4. Найдите отношение длины большей стороны листа формата А1 к меньшей. Ответ округлите до десятых.

• Ответ

   

  1.4

ЗАДАНИЕ 5. Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А3 так же, как этот же текст, напечатанный шрифтом высотой 15 пунктов на листе формата А4? Размер шрифта округляется до целого.

• Ответ

   

  21

ЗАДАНИЕ 6. Найдите значение выражения

• Ответ

   

  2.1

ЗАДАНИЕ 7. На координатной прямой отмечены точки 𝐴, 𝐵, 𝐶 и 𝐷. Одна из них соответствует числу √60. Какая это точка?

• Ответ

   

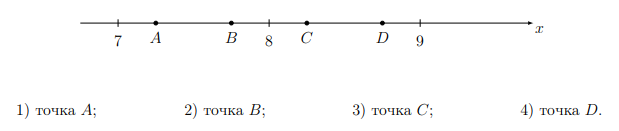
  2

ЗАДАНИЕ 8. Найдите значение выражения √︀49𝑥8𝑦4 при 𝑥 = 2 и 𝑦 = 3.

• Ответ

   

  1008

ЗАДАНИЕ 9. Решите уравнение 9𝑥2 = 54𝑥. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

• Ответ

   

  0

ЗАДАНИЕ 10. В фирме такси в данный момент свободно 30 машин: 1 чёрная, 9 жёлтых и 20 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.

• Ответ

   

  0.3

ЗАДАНИЕ 11. Установите соответствие между функциями и их графиками.

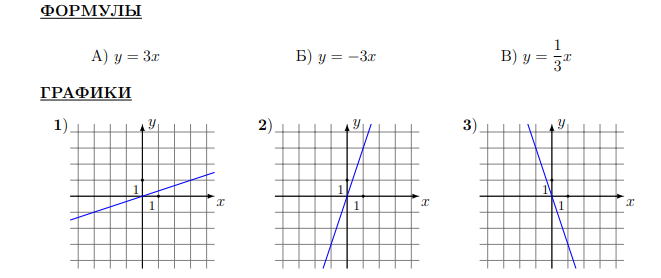
В таблице под каждой буквой укажите соответствующий номер.

В ответе укажите последовательность трёх цифр.

• Ответ

   

  231

ЗАДАНИЕ 12. Центростремительное ускорение при движении по окружности (в м/c2 ) можно вычислить по формуле 𝛼 = 𝜔 2𝑅, где 𝜔 — угловая скорость (в 𝑐 −1), а 𝑅 — радиус окружности. Пользуясь этой формулой, найдите радиус 𝑅 (в метрах), если угловая скорость равна 9 c−1, а центростремительное ускорение равно 243 м/c2. Ответ дайте в метрах.

• Ответ

   

  3

ЗАДАНИЕ 13. Укажите неравенство, решение которого изображено на рисунке 𝑥−7 7

• Ответ

   

  1

ЗАДАНИЕ 14. У Яны есть попрыгунчик (каучуковый шарик). Она со всей силы бросила его об асфальт. После первого отскока попрыгунчик подлетел на высоту 240 см, а после каждого следующего отскока от асфальта подлетал на высоту в два раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит попрыгунчик, станет меньше 5 см?

• Ответ

   

  7

ЗАДАНИЕ 15. Найдите острый угол параллелограмма 𝐴𝐵𝐶𝐷, если биссектриса 𝐴𝐾 угла 𝐴 образует со стороной 𝐵𝐶 угол, равный 33∘. Ответ дайте в градусах.

• Ответ

   

  66

ЗАДАНИЕ 16. Сторона равностороннего треугольника равна 2√3. Найдите радиус окружности, описанной около этого треугольника.

• Ответ

   

  2

ЗАДАНИЕ 17. Периметр ромба равен 36, а один из углов равен 30∘. Найдите площадь этого ромба.

• Ответ

   

  40,5

ЗАДАНИЕ 18. На клетчатой бумаге с размером клетки 1 × 1 изображён прямоугольный треугольник. Найдите длину его большего катета.

• Ответ

   

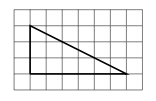
  6

ЗАДАНИЕ 19. Какие из следующих утверждений верны?

1. Все углы прямоугольника равны.
2. Боковые стороны любой трапеции равны.
3. Площадь квадрата равна произведению двух его смежных сторон.

• Ответ

   

  13

ЧАСТЬ 2.

ЗАДАНИЕ 20. Решите систему уравнений

• Ответ

   

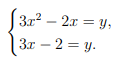
  (1; 1) (2/3; 0)

ЗАДАНИЕ 21. Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 70 км/ч, а вторую половину пути проехал со скоростью, большей скорости первого автомобилиста на 21 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста.

• Ответ

   

  84

ЗАДАНИЕ 22. Постройте график функции

𝑦 = |𝑥|(𝑥 + 1) − 2𝑥.

Определите, при каких значениях 𝑚 прямая 𝑦 = 𝑚 имеет с графиком ровно две общие точки.

• Ответ

   

  -025; 2.25

ЗАДАНИЕ 23. Отрезки 𝐴𝐵 и 𝐶𝐷 являются хордами окружности. Найдите длину хорды 𝐶𝐷, если 𝐴𝐵 = 10, а расстояния от центра окружности до хорд 𝐴𝐵 и 𝐶𝐷 равны соответственно 12 и 5.

• Ответ

   

  24

ЗАДАНИЕ 24. Известно, что около четырёхугольника 𝐴𝐵𝐶𝐷 можно описать окружность и что продолжения сторон 𝐴𝐵 и 𝐶𝐷 четырёхугольника пересекаются в точке 𝑀. Докажите, что треугольники 𝑀𝐵𝐶 и 𝑀𝐷𝐴 подобны.

• Ответ

   

  6

ЗАДАНИЕ 25. В треугольнике 𝐴𝐵𝐶 биссектриса угла 𝐴 делит высоту, проведённую из вершины 𝐵, в отношении 5 : 4, считая от точки 𝐵. Найдите радиус окружности, описанной около треугольника 𝐴𝐵𝐶, если 𝐵𝐶 = 12.

• Ответ

   

  10